When Does the Limit Comparison Test Fail
Suppose the limit is less than 1 and pick a number r larger than the limit but still less than 1 for instance the average of the limit and 1. - McGregor Support when does the integral test fail.
Series Convergence Tests Series Review
Instead of comparing to a convergent series using an inequality it is more flexible to compare to a convergent series using behavior of the terms.

. Show activity on this post. If we know one of the series was convergent then the other converges as well. N 1 5 n 3 7 n 2 9 n 6 2 n 3 1.
Consider the alternating series -1 1-14-- a. So for all n equal to k k plus one k plus two on and on and on and on and and this is the key this is where the limit of the Limit Comparison Test comes into play and if the limit the limit as n approaches infinity of a sub n over b sub n b sub n is positive and finite is positive and finite that either both series converge or. The root test works whenever the ratio test does but the limit involved in the root test is often more difficult from a practical perspective.
This is more of an art than a science that is sometimes you have to try several things in order to find the. There are useful variants of the comparison tests. The idea of this test is that if the limit of a ratio of sequences is 0 then the denominator grew much faster than the numerator.
Use partial fraction decomposition. Answer 1 of 2. N 1 n 1.
Because we got a limit of 1 we. When youre looking at a positive series whats the best way to determine whether it converges or diverges. Lets formalize this with limit comparison.
P lnn n2 P 1 n2 Go back and read scenario iii of the limit comparison test carefully. N1 nn 312n n 1 n n 3 1 2 n. While the integral test is a nice test it does force us to do improper integrals which arent always easy and in some cases may be impossible to determine the.
We conclude with an example where nding gx. The Limit Comparison Test is a good test to try when a basic comparison does not work as in Example 3 on the previous slide. If and converges then converges.
So we have obtained. Since frac1nn equiv frac1x32 this is a convergent p-series. Dividing by 3 n we are left with.
This application of the Comparison Test is trickier still. What test to use. The limit comparison test does not apply because the limit in question does not exist.
In general the Ratio Test will fail if the general term is a rational function. In the previous section we saw how to relate a series to an improper integral to determine the convergence of a series. Lets take a look at a couple of examples.
Free Series Limit Comparison Test Calculator - Check convergence of series using the limit comparison test step-by-step This website uses cookies to ensure you get the best experience. Section 4-7. Then because the limit is less than r for all n at least as large as some positive integer N we have a n1a n r ie a n1 a nr.
Notice that the Ratio Test considers the ratio of the absolute values of the terms. In this case limit comparison is a better choice. So lets think of two.
3 points Use the Limit Comparison Test to determine whether the following series converges or diverges S 20-8 7. The limit is a finite positive number. The limit comparison test LCT differs from the direct comparison test.
If L 1 or the limit goes to then a n diverges. But when I attempt to prove this by the limit comparison test with known convergent series such as sumlimits_n1 frac1n2 ex. Remember for limit comparison we take the expressions in the two series we are comparing and form the ratio.
The limit comparison test eliminates this part of the method. Lim_n to fracfrac1nnfrac1n2 The limit comparison test does not prove this fact. Comparison TestLimit Comparison Test.
Alternating series test for convergence. The limit comparison test eliminates this part of the method. It may be one of the most useful tests for convergence.
It seems to be very similar. If a n blows up and the b n are bigger than the a n then b n blows up. The limit comparison test for series convergence.
To evaluate this equation first notice that n. Divide every term of the equation by 3 n. The Limit Comparison Test Let and.
By using this website you agree to our Cookie Policy. Taking the dominant terms this reduces to 1 n 3 which converges. Lim nn1 n 1 lim n.
We say the Ratio Test fails if L 1. 2 points Which of the two conditions of the Alternating Series Test does this series fail. Donors can also give by check payable to.
Example 1 Determine if the following series is convergent or divergent. Lim x1 fx gx lim x1 5 2sinxx32 1x32 lim x1 5 2sinx. If L 1 or if L does not exist then this test is inconclusive and we must do more work.
Since Ill compare the given series to. There really isnt much to these problems other than computing the limit and then using the root test. The comparison test can be used to show that the original series converges.
SAMS-USA PO Box 399 Ambridge PA 15003. The limit comparison test shows that the original series is divergent. Converges since its a p-series with.
If and diverges then diverges. If then either both series converge or they both diverge. The Limit Comparison Test.
Just want to make sure Im applying the limit comparison test correctly. Thus the test fails and we must resort to a direct comparison. In a situation like this you cannot just ignore the lnn and run comparison against 1 n2.
The nal limit does not converge because the sine function has no limit as x1. Lim n1 lnn n2 1 n2 lim n1 lnn 1. Functions are positive on 11 so we then try to compute the limit necessary to apply the limit comparison test.
Using the comparison test can be hard because finding the right sequence of inequalities is difficult. The comparison test can be used to show that the original series diverges. The limit comparison test is an easy way to compare the limit of the terms of one series with the limit of terms of a known series to check for convergence or divergence.
Multiply by the reciprocal of the denominator. If a n is bad and 0 a n b n for all n then b n is bad. And if so and it does indeed fail what should be my next step in determining if the series diverges.
If the limit is infinity the numerator grew much faster. Suppose lim sup. Video transcript - Voiceover So lets get a basic understanding of the comparison test when we are trying to decide whether a series is converging or diverging.
If the limit L of that ratio as n - inf exists and is greater than 0 then the test is conclusive. Using the comparison test can be hard because finding the right sequence of inequalities is difficult. For one thing what happens for small n doesnt matter.

Direct Comparison Test Video Khan Academy

How To Use The Limit Comparison Test To Determine Whether A Series Converges Dummies
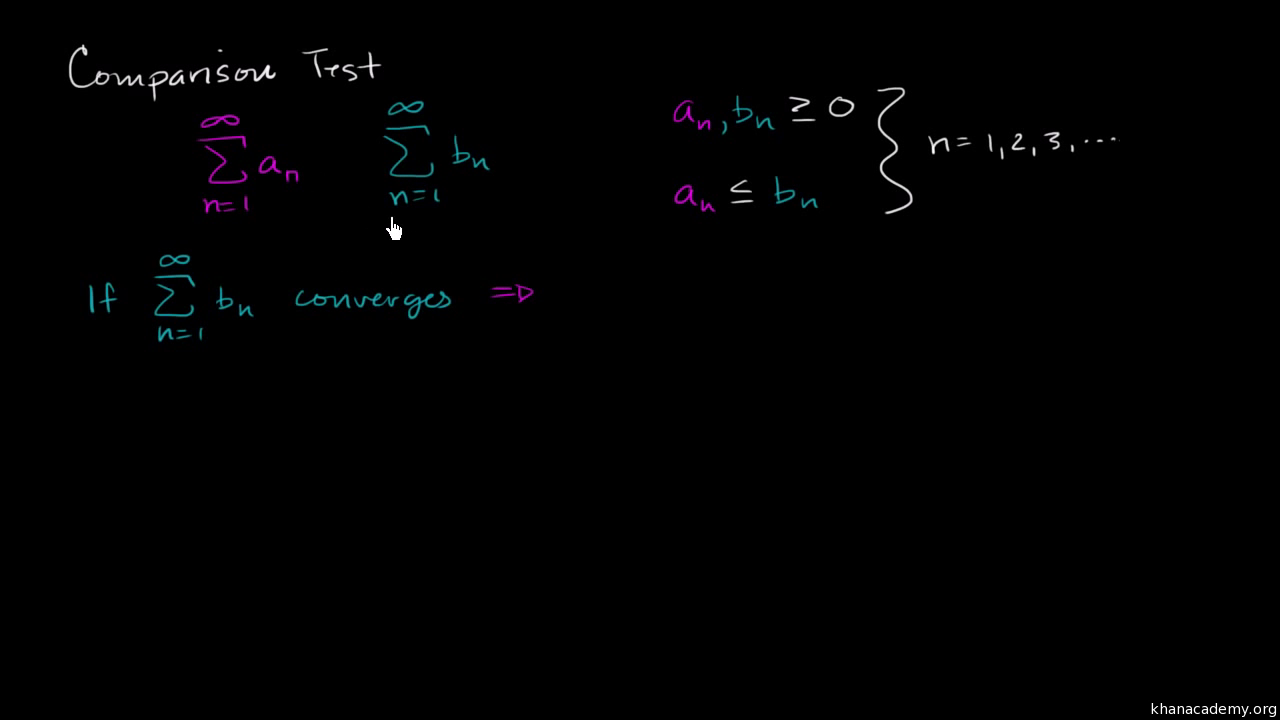
Direct Comparison Test Video Khan Academy

9 4 Day 2 Limit Comparison Test Ppt Video Online Download

9 4 Day 2 Limit Comparison Test Ppt Video Online Download

9 4 Day 2 Limit Comparison Test Ppt Video Online Download

Limit Comparison Test Video Khan Academy

9 4 Day 2 Limit Comparison Test Ppt Video Online Download
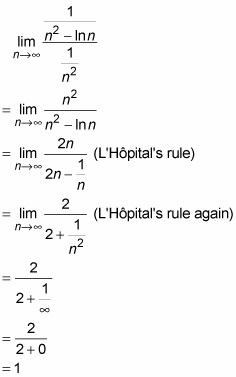
How To Use The Limit Comparison Test To Determine Whether A Series Converges Dummies

9 4 Day 2 Limit Comparison Test Ppt Video Online Download

Alternating Series Test Video Khan Academy
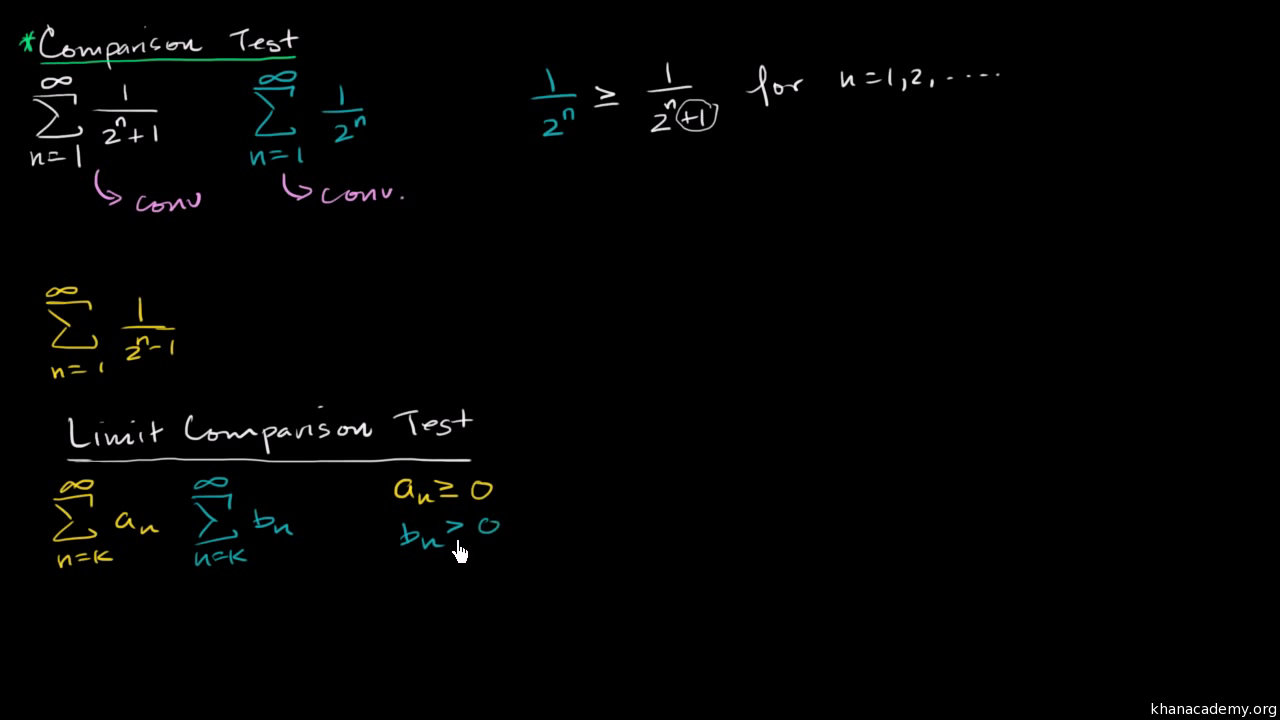
Limit Comparison Test Video Khan Academy






Comments
Post a Comment